Sometimes You Just Need a Math Prodigy to Explain the Quotidian Uses of the Fourth Dimension

When mathematicians talk about the fourth dimension, we’re not talking about time. We’re talking about a fourth geometric dimension, just like the first three. There’s up-down, left-right, forward-back, and then, let’s say, “flim-flam.” You know, another one.

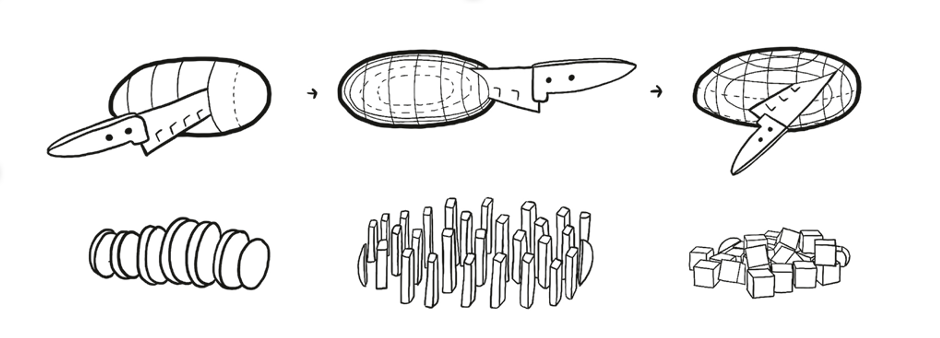
It’s pretty clear from looking around, though, that our world has only three spatial dimensions. Don’t take my word for it—look at the evidence. If you want to slice a potato into tiny pieces, you need to hold the knife in three different directions.

Another way to tell: Imagine you could travel in only two directions. Most of space would be off-limits to you. Any two directions sweep out only a flat plane of motion. 

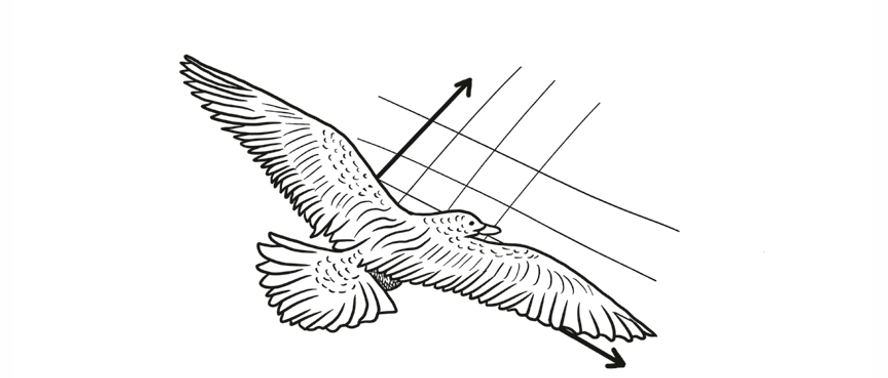
But if you add a third direction, you can travel the whole sky. It takes three directions to cover a three-dimensional space.

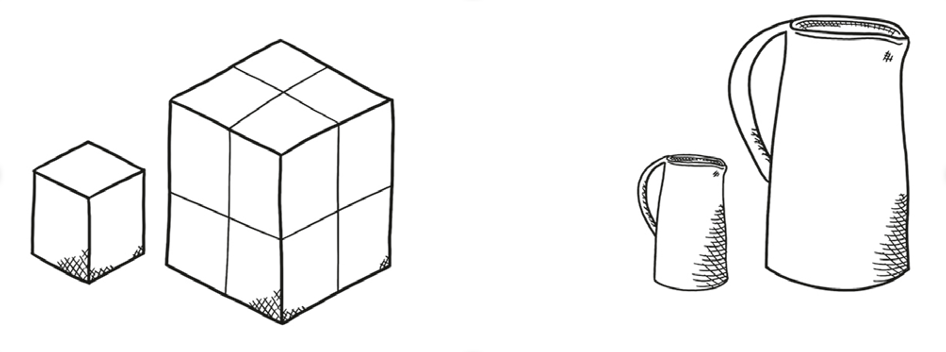
One more clue: Consider a jug of any size and shape. If you make a scale replica that’s exactly twice as big, it’ll hold exactly eight times as much water—double for each dimension.

What’s the use of talking about an imaginary fourth dimension when we’re sure we only have three? Why not just classify the manifolds up to three dimensions and call it a day? I can offer two responses: one from a pure mathematician and one from an applied mathematician.

To a pure mathematician, the question is missing the point. We’re not classifying manifolds to be useful. We’re just curious what possible different types of shapes can exist! We don’t have to constrain ourselves to this arbitrary world we happen to live in. Math is general, universal—it’s not made in our image. So we have three dimensions. And? We have ten fingers, and do we stop counting there? 

That list of sheet-manifolds was out there, somehow, before we ever wrote it down, and it’ll still be the complete list of sheet-manifolds long after our civilizations are lost to history. If that alone doesn’t make you curious about what types of manifolds exist in higher dimensions, just because they aren’t useful, well then you weren’t really in it for the right reasons to begin with.

Then the applied mathematician comes along and ruins everything by making topology useful.

As it happens, knowing about the topological manifolds is actually useful in quite a few contexts. Yes, even the higher-dimensional ones! It’s not why the field was developed, or why people still work on it today, but the language and toolset of topology come in handy pretty often when analyzing aspects of the real world.

The reason it’s useful: Humans tend to be visual thinkers, so we often make visual analogies to help us understand abstract ideas. Our everyday languages are so filled with visual analogies that we don’t even notice we’re using them: You “move forward” on a project, the rents “go up,” and an endless argument goes “in circles.” When we make these analogies, we’re translating real-life problems into topology problems.

Think about politics, for example. Political ideology is a highly complex thing, and it’s not always obvious how to compare and contrast two people’s beliefs in a concise way. To simplify things, it’s common to put ideology on a left-right axis, with progressive, liberal, egalitarian ideals on the left, and traditional, conservative, libertarian views on the right. 

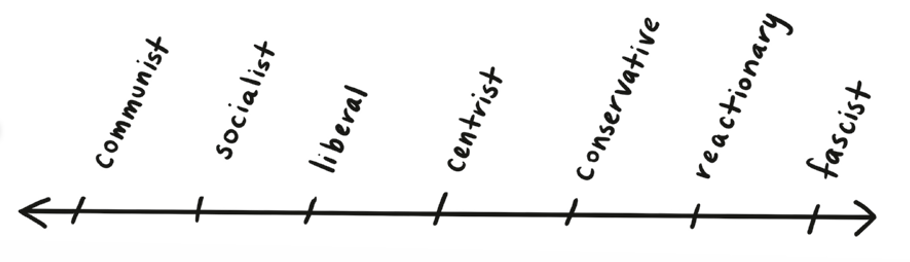
This isn’t a perfect system, but it’s a useful visual analogy. We can now ask difficult, multifaceted questions in basic, visual terms: “Who’s further left on workers’ rights?” And sure, we’ve lost a lot of detail—nothing in the real world is ever as clean and bare as the abstract world of topology—but a lot of what matters is preserved.

Once you’ve set up a visual analogy like this, you have access to all the language and tools of topology. You can wonder which space is the best representation of the system: Is it a circle or an infinite line? In other words, is ideology cyclical, or can you always move further to the left and right? Or are there special points? Are there “true left” and “true right” positions, and everyone is somewhere in the middle?

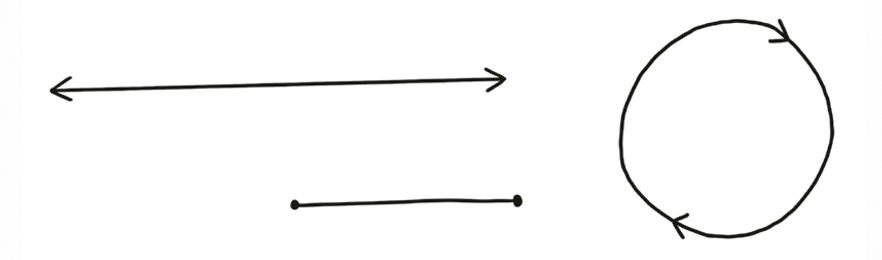
Or maybe we should think there are more dimensions to political ideology than just a single left-right axis. Some people say they’re socially liberal and fiscally conservative at the same time. That would mean that ideology space is at least two-dimensional. If that’s true, which two-dimensional manifold are we dealing with? Do both axes extend to infinity, like a plane? Does one loop around, making an infinite cylinder? Do they both loop around, like a torus? (Okay, they probably don’t both loop around like a torus.)

These questions can be more than just interesting curiosities. If you have some specific goal that has to do with people’s ideologies—predicting how people will vote, maybe, or trying to find supporters for a ballot initiative—then having a good model of ideology space is an important tool. Political campaigns use opinion polling to estimate the distribution of voters across an ideology space, and then use these models to tailor their messages and win voters. Political scientists have found a general way to use legislators’ voting records to predict how they’ll vote in the future, and it works by automatically placing each legislator in a two-dimensional ideology space.

This is how the classification of manifolds is applied outside of math. You only have to solve the abstract math problem once, and then any time you’re using a visual analogy to discuss something, the list of spaces to choose from is always the same.

And I really can’t stress this enough: We use visual analogies all the time. Temperatures rise and fall. Incomes can be low or high or through the roof. December is a long way away, and then it’s approaching, and then it flies by, and then it’s behind us. All these idioms represent the state of some system as a point in a conceptual space, and then describe changes in that system as physical motion through that space.

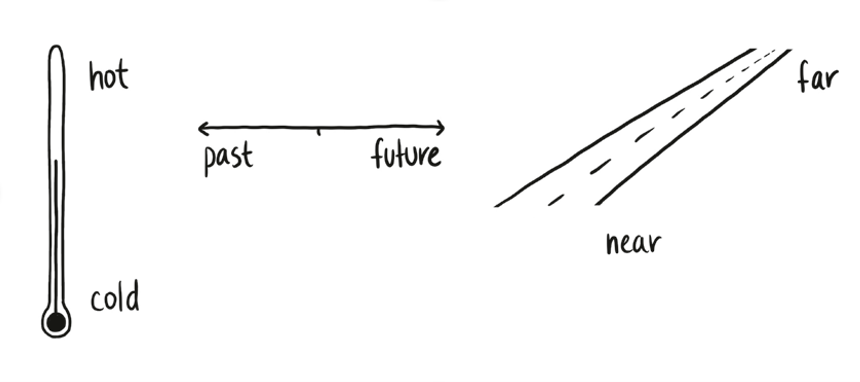
All these examples are one-dimensional, but there can still be interesting topological questions to ask. Does temperature extend forever in both directions, or is there an absolute cold or absolute hot? Does time continue forever to the future, or will there be a Big Crunch? Or does it loop around, so if we wait it out long enough we’ll end up in the distant past?

For more complicated concepts, we need to use the higher-dimensional manifolds. Granted, it’s pretty rare that we actually need to use the fancier manifolds—the real projective plane, or the triple torus, or the crazy undiscovered manifolds in dimension four. (These come up sometimes in physics, but that’s about it, as far as I know.) Most of the systems we come across in our everyday life are well-described by basic, flat spaces: the line, plane, three-space, and so on. In these cases, when we’re trying to understand a system, the main topological question is just: “How many dimensions does it have?”

That’s the question hiding under the surface in a lot of debates across different areas of discourse. We have some concept. How many dimensions does it have?

When you say that gender is a spectrum rather than a binary, that’s a topological claim: You’re saying gender space is one-dimensional (a line) rather than zero-dimensional (two separate points). Or maybe you think it’s a higher-dimensional space, and the feminine-masculine axis is one axis of difference among many. Questions about which conceptual paradigm to use sometimes boil down to questions of dimensionality.

At this point I’m just going to spend the rest of the chapter going through several examples of conceptual spaces and wondering how many dimensions they might have.

Let’s start with personality. Clearly different people have different personalities, and people’s personalities can be compared and can change gradually in all the sorts of ways that suggest we might want to use a visual analogy. So what are the dimensions of personality? How can we break down personality into components?

__________________________________

From Math Without Numbers by Milo Beckman, published by Dutton, an imprint of The Penguin Publishing Group, a division of Penguin Random House, LLC. Copyright © 2021 by Milo Beckman.